Author: siukwan

相关文章：
智力拼图问题–关于回溯和并行：单线程到多线程再到GPU编程的进阶（一）
智力拼图问题–关于回溯和并行：单线程到多线程再到GPU编程的进阶（二）
智力拼图问题–关于回溯和并行：单线程到多线程再到GPU编程的进阶（三）

这次介绍直立拼图问题的详细算法实现。

一、图形的数据结构

我采用了stl里面的vector来进行图形存储，并利用了C++11标准里面的大括号初始化来简化实现，如下：

 

每个图形都是一个二维数组vector<vector<char>> ，因为bool也是占用一个字节，char也是占用一个字节，为了统一矩阵和图形的打印、旋转等函数，统一使用vector<vector<char>>来存储。由于采用vector，所以我们轻易的得到每个图形的长宽。

二、矩阵的数据结构

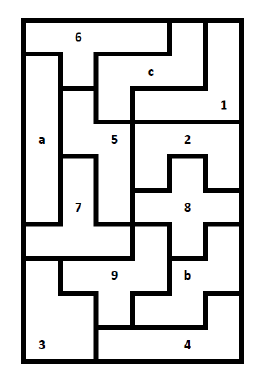
如上面描述，采用vector<vector<char>>进行存储，实验时，实际填充效果如下：
133399
133996
111796
c77766
ccc786
a5c888
a5bb84
a55bb4
a252b4
a22244

使用char字符来存储，初始化矩阵的每个参数都是0，注意是0不是’0’，那么我们检测某个坐标是否被填充时，直接判断该位是0还是非零即可，非零表示已经被填充。

三、深度搜索算法的框架：

 

四、图形如何填充到矩阵mat中？

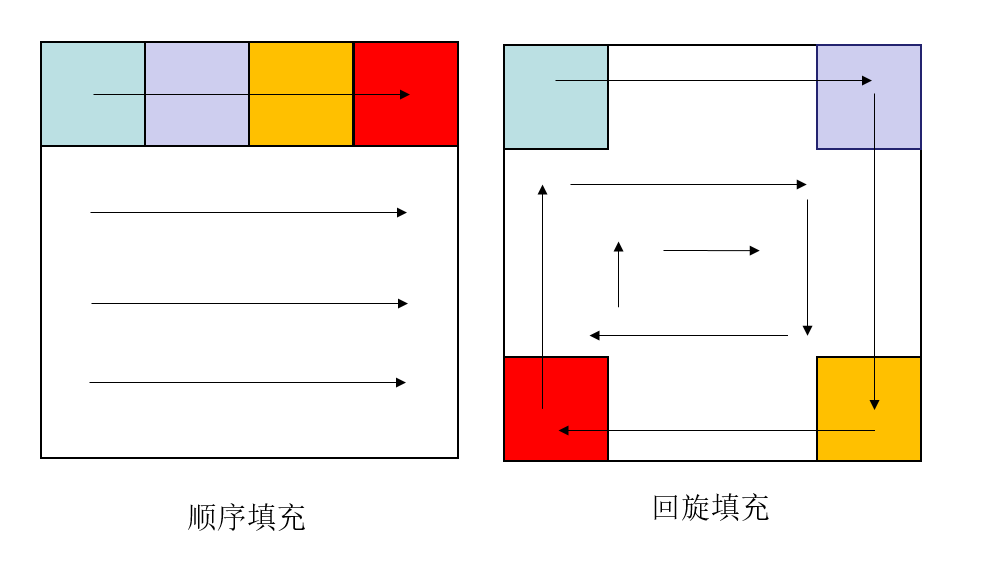
我们采用的是顺序填充算法，即首先搜索出矩阵第一个未被填充的空格，如下图：

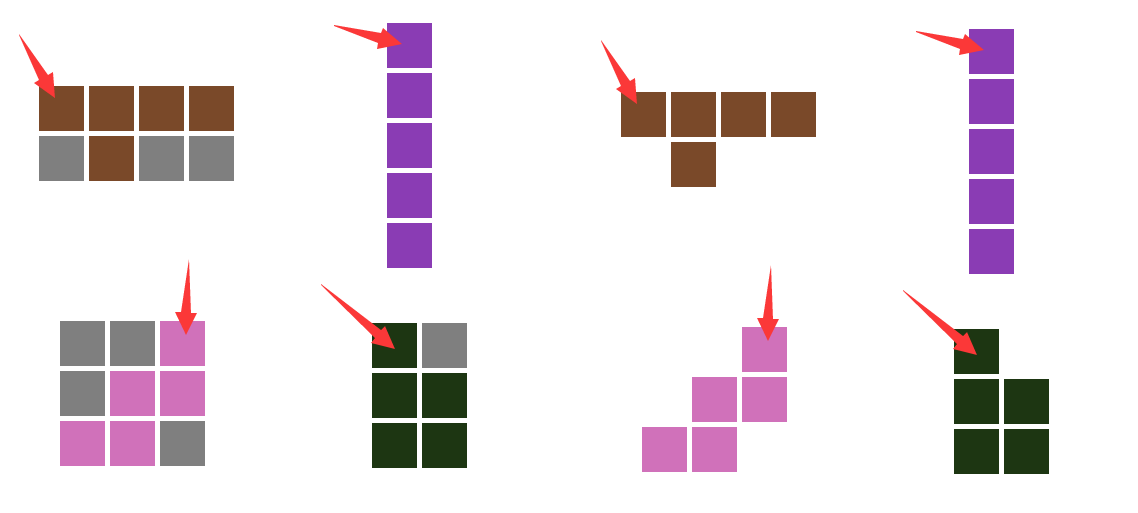
我们知道矩阵的第一个未填充坐标，那么如何把图形填充上去？所以，我们还需要求出图形的第一个有数据的坐标，即第一个为1的位置，如下图红圈的标注：

 

如下面的箭头指示，灰色表示空白部分。

 

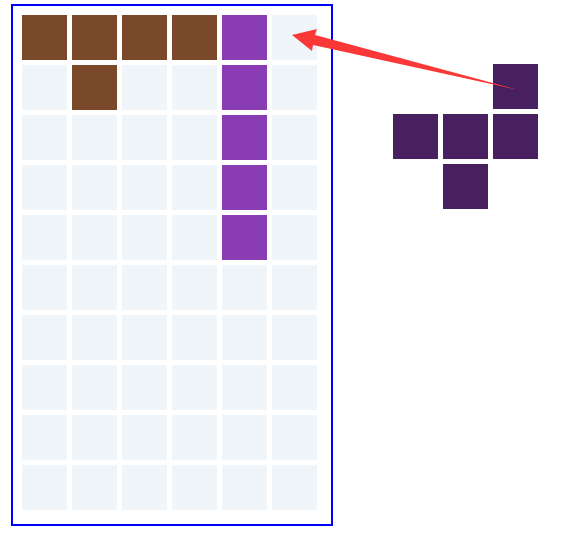
那么，我们有了矩阵的第一个未填充的位置，和图形的第一个有数据的的格子，只要把这个格子对着矩阵的未填充的位置填上去即可，如下图：

填充后：

 

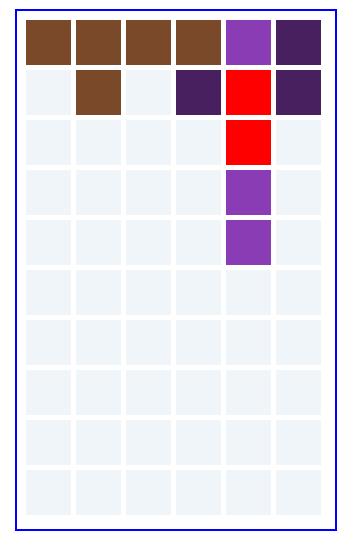
红色部分为冲突部分，证明填充不成功。

 

五、单线程实现

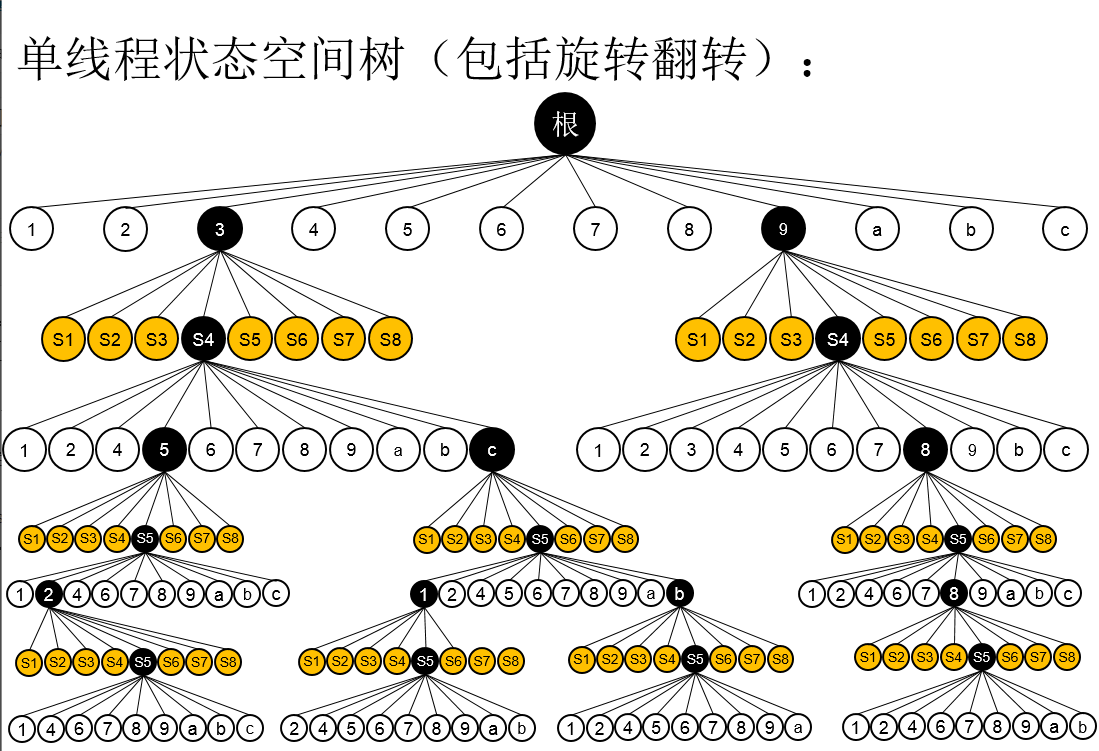
单线程实现较为简单，相当于写一个深度搜索的递归程序。状态空间树如下，实际上这是不够准确的，因为每个节点有多种变形，下面为了简化只画了4层。上面的深度搜索代码框架就是根据单线程画的。

下面为更加准确的一个版本，每个节点包括了8种状态，但是后面为了简化表现，在画图的时候省去了这8种状态。

六、多线程实现

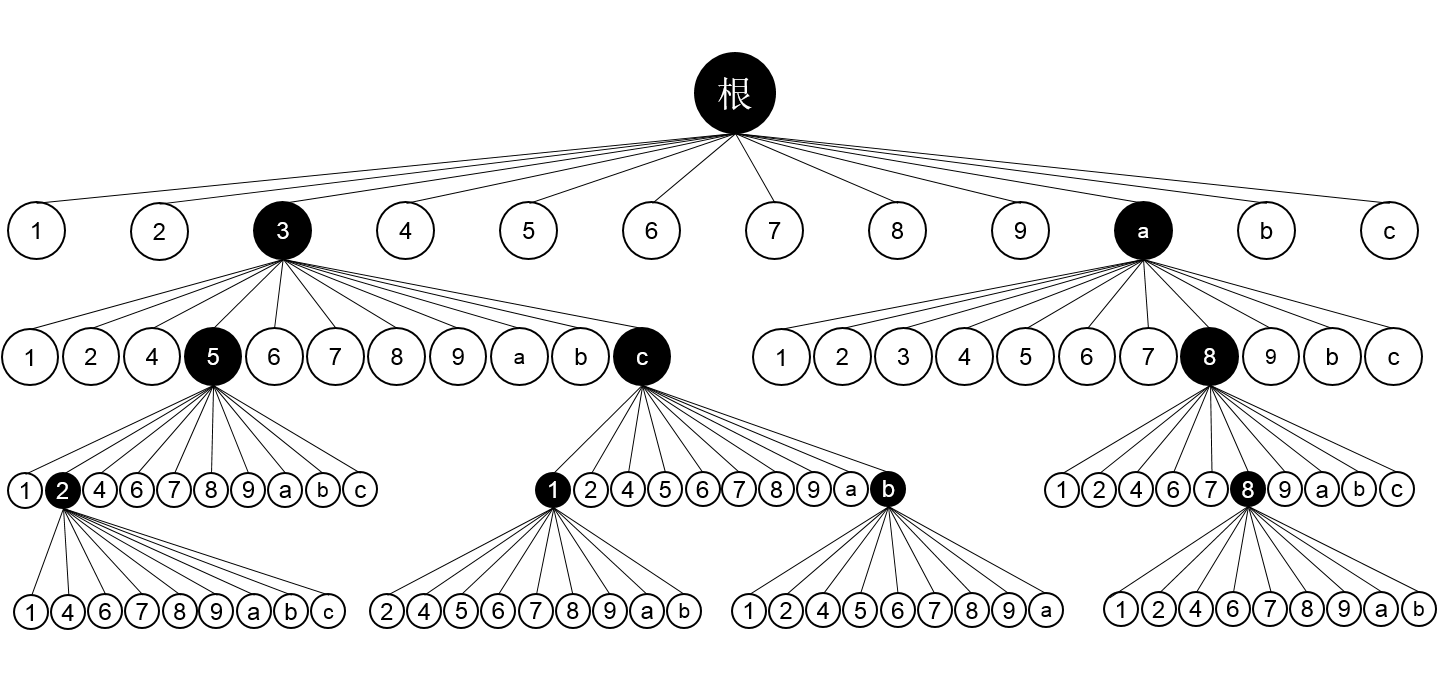
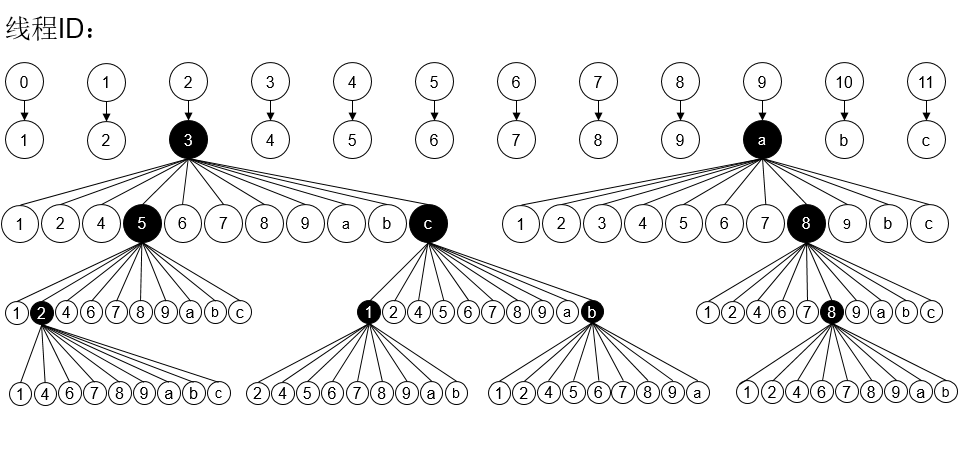
多线程实现，首先是要看电脑的CPU支持多少线程，我们的实验机器cpu是i7-4790K，是四核心八线程的，那么理论上最好是开7条线程，其中一条主线程用来检测7线线程的完成情况，一旦有线程工作完成并结束，马上开启另外一条。对于这道题目，我们可以把状态空间树的第一层（包含123456789abc节点的），分别划分为12条线程。如下图：

七、关于多线程的调度与优化问题

在六中，我们划分为12条线程，选取其中7条，先执行。但是实际上，这相当于人工调度线程，我们需要考虑挑选哪7条线程首先执行？按照顺序进行还是特意筛选？

按照顺序，先执行0到6号线程，那么可能在7到11号线程中，有些线程执行时间相当久，假设0到6号的线程执行时间为1个单位时间，7号线程执行时间为2个单位时间，其余的为1个单位时间，那么顺序执行线程，理论上最终需要3个单位时间。而假如我们先执行线程7，那么最终只需要2个单位时间。

特意筛选，这种方法有个明显的缺陷，就是假设初始化12个图形改变后，我们需要再次进行人工筛选。

那么最好的方法是什么？我们知道实验的电脑支持8线程，而实际上，电脑除了单纯执行我们的程序，还会执行其他的程序。线程数是超过8的，那电脑仍然能够运行起来，是因为操作系统本身就具有线程调度的功能。而实际上，我们只划分了12条线程，而不是12*11=132条线程，同时开启12条线程，CPU的上下文切换并没有占用太多的时间，对我们来说是可以接受的。

实际实验发现，状态少的线程会明显优先结束，CPU似乎是使用了时间片轮转的方法来执行线程。

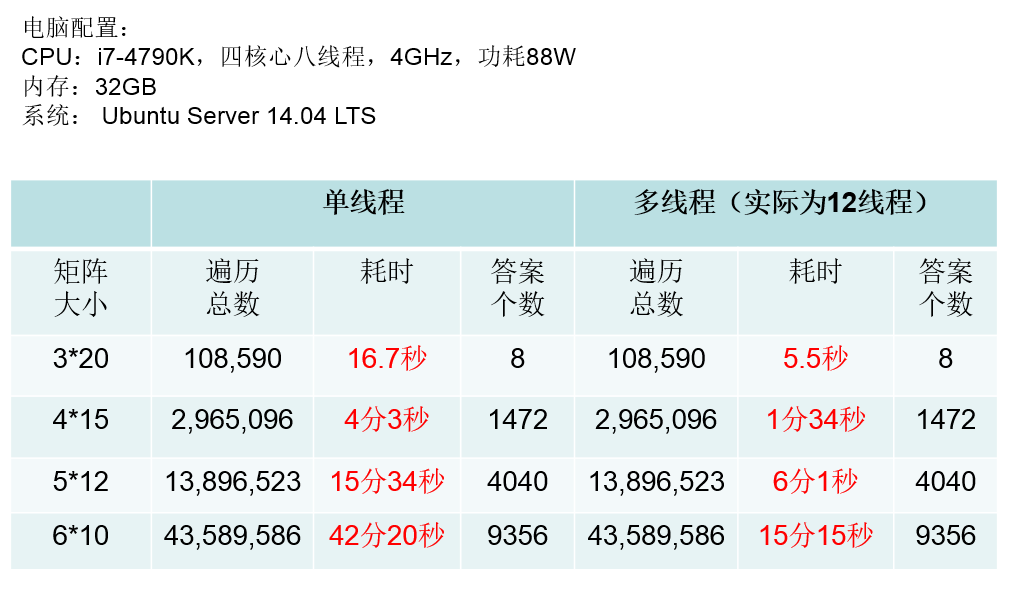
八、实验数据对比

遍历总数和答案个数一致，证明两个算法是正确的，其中主要关注运行时间即可，减少超过一半的运行时间。

 

九、源代码

由于编写的源代码兼容了windows和linux系统，并且兼容了单线程和多线程，代码较长，放在了github上面，网址为：https://github.com/siukwan/algorithm

十、更多的思考

经过上面的讨论，我们发现，这道题目的解法只有回溯（和暴力搜索没什么区别），但是通过改为多线程，我们看到了效率明显提升。既然要涉及到多线程编程，除了找核心更多的CPU还有别的方法吗？没错，多线程编程，实则和并行计算非常接近，既然涉及到并行计算，怎么可以忽略Nvdia的显卡！恰好我的电脑配置了4GB显存的GeForce 840M显卡，性能虽然中等，但是可以尝试！

在下一篇文章中我将会介绍如何把上面的问题通过GPU编程解决：
智力拼图问题–关于回溯和并行：单线程到多线程再到GPU编程的进阶（三）

 

相关文章：
智力拼图问题–关于回溯和并行：单线程到多线程再到GPU编程的进阶（一）
智力拼图问题–关于回溯和并行：单线程到多线程再到GPU编程的进阶（二）
智力拼图问题–关于回溯和并行：单线程到多线程再到GPU编程的进阶（三）

最近算法设计上面有一个回溯的题目，要求使用回溯算法解答，题目如下：

智力拼图问题

设有12个平面图形（1,2,3,4,5,6,7,8,9，a,b,c）如下图所示。每个图形的形状互不相同，但它们都是由5个大小相同的正方形组成。如下图中这12个图形拼接成一个6*10的矩阵。设计一个算法，计算出用这12个图形拼接成给定矩形的拼接方案。

 

题目限制并没有很明确，但是通过网上搜索，可以知道有如下要求：

（1）12个图形就是上图所展示的图形；

（2）这些图形可以进行旋转（每次旋转90°）或者翻转；

（3）每个图形使用1次。

（4）矩阵的形状不一定为6*10，但是面积一定为60，即可以出现3*20，4*15，5*12等等的情况。

一、分析：

先对题目进行简单的分析，由浅到深：

（1）题目需要求出拼接方案，我们默认求出所有的拼接方案，那么没有办法使用动态规划或者贪心算法进行求解，只能够使用深度搜索，进行适当的剪枝。

（2）我们先考虑没有旋转和翻转的情况，那么这12个图形的排列组合情况一共有12!这么多，即479001600种。我们假设每秒遍历1000种组合情况，那么求解需要最多47900.16秒，换算一下，大概约13个小时。假如每秒遍历10万种情况，那么只需要7.98336分钟，约8分钟。实际上深度搜索的过程中，可以进行剪枝，所以运行时间远小于这个值。下面是6*10的矩阵，在图形没有旋转和翻转的情况下，所花费的时间：

只有1秒，因为没有旋转，很容易就剪枝了。

（3）经历了上面的推算，我们尝试加入旋转和翻转，假设每个图像都可以进行旋转和翻转，那么每个图形都可以演化为8种情况，旋转0°+不反转，旋转0°+反转，旋转90°+不反转，旋转90°+反转。。。。。那么总的排列组合情况有12!*8^12，12!（479001600）在2^28（268435456）和2^29（536870912）之间，而8^12相当于2^36，把12!当作2^28，那么总的排列组合数量为2^28*2^36=2^64。

2^64是不是一个很熟悉的数字？没错，就是汉诺塔传说中的64个金片，每秒移动一个金片总共需要5845亿年，好吧，我们的计算机处理速度会更快，那么每秒遍历1000万种情况，那么仍需5.845万年！

当然，实际上会剪枝的，这个只是给大家一个概念。

二、如何剪枝：

（1）从排列组合来看，12!*8^12种，实际上，有些图形旋转或者翻转后是重复的。例如题目图中的8号图形，无论怎么旋转或者翻转，都是一样的，那么遍历的时候，不用再去遍历它旋转或者翻转的情况。同样，1号和a号图形等等，在旋转或者翻转的时候都存在重复的情况，我们可以把这些重复的情况去掉，这样8^12就可降下来了。

（2）第二个剪枝的情形属于正常的遍历排除，我们一个一个图案填充上去，即时检测是否能够填充，能够填充的就继续进行DFS，不能填充的就遍历下一个图形。

（3）会有帮助但是效果不是很明显的剪枝，在实际的填充过程中，我们发现，矩阵填充出出现一些孤立的连通区域，面积为1、2、3等等。实际上，我们每个图形的面积为5，那么假如矩阵出现面积小于5的连通区域，那这个方案也不用再继续DFS了。实际上，要检测连通区域，就会涉及到并查集，而并查集通过递归（也可以改成循环）进行集合的检测和划分，但是对于每种遍历的情况都使用并查集去划分搜索连通区域，会大大地增加时间复杂度。

简化的版本就是，搜索出矩阵的第一个未被填充的空格坐标，检测这个坐标的上下左右（实际上只检测下右即可）是否已经被填充，如果被填充就return，没有被填充就继续DFS。这个版本实际上是检测单个的面积为1的连通区域，对剪枝是有帮助的（实际上帮助比较少），而且只是多加两个判断，对时间复杂度影响不大。

（4）除了上述的剪枝，我们还尝试另外一种填充方法。我们默认的填充方法，称之为顺序填充，是从左到右从上到下依次填充，这样做的缺点就是下方空余的连通区域较大，不利用使用（3）的方法进行剪枝。如何更好地利用（3）方法进行剪枝呢？我们提出了一种回旋填充的方法，一次填充4个角，这样可以从外围往中间逼近，从而更容易产生比顺序填充更小的连通区域。这些更小的连通区域就更有可能适合方法（3）的剪枝。

但是，通过实践证明，回旋填充会导致更加糟糕的时间复杂度。我们进行了对比实验，对6*10的矩阵进行填充。我们填充6*10的矩阵，使用单线程的DFS，总共需要耗时38分钟，答案个数为9356个，总共遍历了4358万种情况（省去了万位以下的数字）。而使用回旋填充的方法，我们填充6*10的矩阵，遍历71分钟后（程序并未结束），只搜索到了99个答案，遍历了5800万种情况。那么保守估计，等到遍历出9356个答案，大约需要再花费71*10分钟（假设每71分钟遍历出99个答案），遍历的情况总数将会远超4358万种。

仔细分析，每个图形只占用了5个面积，而矩阵的面积为60！进行回旋填充，我们期望出现面积为1的连通域，需要填充多次。而相比之下，回旋填充相当于选择了更为广阔的空间进行图形的填充，而顺序填充由于宽度的限制（例如宽度为3，4，5，6），很容易就对图形判断是否合适。而回旋填充每次选择了空间余量较大的角落进行填充，因此会遍历更多的次数！

 

综上所述，我们只能够利用方法（1）（2）（3）进行剪枝深度搜索，也就是使用回溯法。具体实现：

智力拼图问题–关于回溯和并行：单线程到多线程再到GPU编程的进阶（二）

1.最近在apue编程中，需要规范项目，所以把错误函数统一放到根目录下，整个文件的假如如下图所示：

其中func_err.cpp和func.h是在根目录中，而CMakeLists.txt是在根目录的1stUNIXSystemOverview文件夹中，那么需要连接编译func.h和func_err.cpp时怎么办呢？

包含func.h很简单，直接在代码中include”../func.h”即可。

而连接func_err.cpp在cmake语法中也是一样的，如下：

SET(LIB_FUNC_ERR_SRC  ../func_err.cpp)

在CUDA的GPU编程里面，函数分为三类，前缀分别为__global__、__host__、__device__。

（1）__host__

如果没有标明前缀，那么函数默认为__host__，可以理解为CPU函数，这些函数不能被global和device函数所调用。

（2）__global__

前缀注明__global__，则这个函数可以被GPU调用，并且这个函数可以调用__device__前缀的函数。

（3）__device__

__device__表明这个函数是在GPU里面运行的。

最近在使用cuda平台进行一些多线程的编程，其中涉及到把数据从内存复制到显存，然后从显存复制到内存的操作。其中复制操作有很重要的一点是，假如是复制数组，内存空间必须是连续的。其中一维数组本身是连续的，所以没有问题。但是对于二维数组和三维数组等等，需要一开始就要分配好空间，不能使用new或者malloc来动态分配，否则会出现复制后没有效果，或者其他意想不到的后果。

我刚开始是用动态创建数组的，即new，结果运行程序后，发现cpu_graph没有改变，后来把定义改为确定大小的数组后，才能复制成功。

整个工作流程大概是：

[c language=”++”]
GraphAll *gpu_graph;
//在gpu上分配内存
cudaMalloc((void **)&gpu_graph, sizeof(cpu_graph));
//把数据从内存复制到显存
cudaMemcpy(gpu_graph, &cpu_graph, sizeof(cpu_graph), cudaMemcpyHostToDevice);
//进行数据处理
SiukwanTest(gpu_graph);
//把在gpu中处理完毕的数据从显存复制到内存
cudaMemcpy(&cpu_graph, gpu_graph, sizeof(cpu_graph), cudaMemcpyDeviceToHost);
//释放显存
cudaFree(gpu_graph);
[/c]

刚开始的GraphAll变量定义如下，基本采用了指针，进行动态分配：

[c language=”++”]
struct GraphNode
{
char **shape;
int x ;
int y ;
};
//记录每种图形的变形，原始，旋转，翻转，不除去重复的，共有8种
struct GraphFormat
{
GraphNode *format;
int formatCount;
};
//存储所有图形
struct GraphAll
{
GraphFormat *graph;
int graphCount;
}cpu_graph;//cpu图形定义为全局变量
[/c]

由于进行动态分配，地址空间不连续，导致复制失败。后面我把变量改成确定大小的数组，如下，然后同样的程序，复制成功了：

[c language=”++”]
struct GraphNode
{
char shape[5][5];
int x ;
int y ;
};
//记录每种图形的变形，原始，旋转，翻转，不除去重复的，共有8种
struct GraphFormat
{
GraphNode format[8];
int formatCount;
};
//存储所有图形
struct GraphAll
{
GraphFormat graph[12];
int graphCount;
}cpu_graph;//cpu图形定义为全局变量
[/c]

最近需要写一个回溯的程序，因为最终要提交windows的exe文件，但是测试的时候windows上运行太慢，于是在linux上测试数据。所以导致这个程序需要兼容linux和windows。

我先是通过下面的宏判断来区分windows代码和linux代码：

#ifdef WIN32

#else

#endif

下面再介绍一些windows和linux的多线程编程：

一、windows

windows下面的多线程编程需要用到的函数是
HANDLE hThread = CreateThread(NULL, 0, dfsThread, NULL, 0, NULL);

其中dfsThread是我定义的函数。如果需要加上互斥量，可以通过下面的语句添加：

[c language=”++”]
#include <windows.h>
#include <tchar.h>
HANDLE GraphIdxMutex = CreateMutex(NULL, FALSE, _T("GraphIdx"));
WaitForSingleObject(GraphIdxMutex, INFINITE);//加锁或等待其他线程释放锁
//进行操作
ReleaseMutex(GraphIdxMutex);//释放锁
[/c]

注意CreateMutex函数的第三个参数，它需要LPCWSTR类型，我们可以添加头文件tchar.h，利用_T(“string”)把string（或const char）转化为LPCWSTR。

二、linux

在linux上面，pthread的用法和windows上面的用法十分相似，需要包含<pthread.h>创建线程的函数为：
pthread_create(&tid, NULL, dfsThread, NULL);

其中需要把dfsThread定义为函数指针，例如void *dfsThread（）。

另外，因为pthread不在系统库中，所以编译的时候需要指明使用pthread库，编译语句如下：

[shell]
g++ main.cpp -lpthread -std=c++11
[/shell]

互斥量如下：

[c language=”++”]
pthread_mutex_t GraphIdxMutex;
pthread_mutex_init(&amp;GraphIdxMutex, NULL);//需要初始化
pthread_mutex_lock(&GraphIdxMutex); // 给互斥体变量加锁
//进行操作
pthread_mutex_unlock(&GraphIdxMutex); // 给互斥体变量解除锁
[/c]

下面是dfsThread函数体的定义以及实际创建线程，实现一样的功能：
[c language=”++”]

#ifdef WIN32
//windows多线程
int PrintfThreshold = 1000;

//创建互斥变量
HANDLE RunningThreadSumMutex = CreateMutex(NULL, FALSE, _T("RunningThreadSum"));
HANDLE GraphIdxMutex = CreateMutex(NULL, FALSE, _T("GraphIdx"));

DWORD WINAPI dfsThread(LPVOID lpParamter)
{
//互斥访问GraphIdx，并复制当前的GraphIdx，避免后面出现被其他线程更改的情况
WaitForSingleObject(GraphIdxMutex, INFINITE);
int tmpIdx = GraphIdx;
GraphIdx++;
ReleaseMutex(GraphIdxMutex);

printf("\n|—————————————————————|\n");
printf( "| 开启%02d线程 |\n", tmpIdx);
printf( "|—————————————————————|\n\n");

//进行深度搜索
dfs(0, ThreadUsed[tmpIdx], ThreadMat[tmpIdx], ThreadAnswer[tmpIdx], tmpIdx, ThreadCounter[tmpIdx]);

//线程工作完成
WaitForSingleObject(RunningThreadSumMutex, INFINITE);
RunningThreadSum–;
ReleaseMutex(RunningThreadSumMutex);
ThreadFinished[tmpIdx] = true;

printf("\n|—————————————————————|\n");
printf( "|XXXXXXXXXXXXXXXXXXXXXX 结束%02d线程 XXXXXXXXXXXXXXXXXXXXXXX|\n", tmpIdx);
printf( "|—————————————————————|\n\n");
return 1;
}
#else
int PrintfThreshold = 1000000;

//创建互斥变量
pthread_mutex_t RunningThreadSumMutex;
pthread_mutex_t GraphIdxMutex;

void *dfsThread(void *arg)
{
//互斥访问GraphIdx，并复制当前的GraphIdx，避免后面出现被其他线程更改的情况
pthread_mutex_lock(&GraphIdxMutex); // 给互斥体变量加锁
int tmpIdx = GraphIdx;
GraphIdx++;
pthread_mutex_unlock(&GraphIdxMutex); // 给互斥体变量解除锁

printf("\n|—————————————————————|\n");
printf( "| 开启%02d线程 |\n", tmpIdx);
printf( "|—————————————————————|\n\n");

//进行深度搜索
dfs(0, ThreadUsed[tmpIdx], ThreadMat[tmpIdx], ThreadAnswer[tmpIdx], tmpIdx, ThreadCounter[tmpIdx]);

//线程工作完成
pthread_mutex_lock(&RunningThreadSumMutex); // 给互斥体变量加锁
RunningThreadSum–;
pthread_mutex_unlock(&RunningThreadSumMutex); // 给互斥体变量解除锁
ThreadFinished[tmpIdx] = true;

printf("\n|—————————————————————|\n");
printf("|XXXXXXXXXXXXXXXXXXXXXX 结束%02d线程 XXXXXXXXXXXXXXXXXXXXXXX|\n", tmpIdx);
printf("|—————————————————————|\n\n");
}

#endif

//实际调用：

while (openThreadCount<12)
{//开启12条线程
if (RunningThreadSum < CPU_THREAD_COUNT)
{//开启12条线程，如果能够开线程
#ifdef WIN32
WaitForSingleObject(RunningThreadSumMutex, INFINITE);
RunningThreadSum++;
openThreadCount++;
ReleaseMutex(RunningThreadSumMutex);
//开线程：
HANDLE hThread = CreateThread(NULL, 0, dfsThread, NULL, 0, NULL);
Sleep(1);
#else
pthread_mutex_lock(&RunningThreadSumMutex); // 给互斥体变量加锁
RunningThreadSum++;
openThreadCount++;
pthread_mutex_unlock(&RunningThreadSumMutex); // 给互斥体变量解除锁
//开线程：
pthread_t tid;
pthread_create(&tid, NULL, dfsThread, NULL);
usleep(1);
#endif
}
else//不能开线程
while (RunningThreadSum >= CPU_THREAD_COUNT);
}

[/c]
 

在centOS系统中，可以通过nmap来检测端口、ip使用情况。
Nmap是一款网络扫描和主机检测的非常有用的工具。Nmap是不局限于仅仅收集信息和枚举，同时可以用来作为一个漏洞探测器或安全扫描器。它可以适用于winodws,linux,mac等操作系统

Nmap是一款非常强大的实用工具,可用于：检测活在网络上的主机（主机发现）检测主机上开放的端口（端口发现或枚举）检测到相应的端口（服务发现）的软件和版本检测操作系统，硬件地址，以及软件版本检测脆弱性的漏洞（Nmap的脚本）Nmap是一个非常普遍的工具，它有命令行界面和图形用户界面。

1.先使用sudo yum install nmap命令进行安装。

2.使用nmap

[shell]

nmap 192.168.1.1-100 #扫描IP地址为192.168.1.1-192.168.1.100内的所有主机
nmap localhost    #查看主机当前开放的端口
nmap -p 1024-65535 localhost    #查看主机端口(1024-65535)中开放的端口
nmap -PS 192.168.21.163        #探测目标主机开放的端口
nmap -PS22,80,3306  192.168.21.163    #探测所列出的目标主机端口
nmap -O 192.168.21.163    #探测目标主机操作系统类型
nmap -A 192.168.21.163    #探测目标主机操作系统类型
nmap –help  #更多nmap参数请查询帮助信息

[/shell]

3.关闭或打开主机端口

[shell]
nmap localhost #查看主机当前开放端口
ntsysv #打开系统服务器管理器(需要先安装yum install ntsysv)，选择要关闭或者打开的服务
[/shell]

[shell]
warning: push.default is unset; its implicit value is changing in Git 2.0 from ‘matching’ to ‘simple’.

To squelch this message and maintain the current behavior after the default changes, use: git config –global push.default matching

To squelch this message and adopt the new behavior now, use: git config –global push.default simple
[/shell]

出现这个提示，但是实际上，git还是会提交。

可以按照上述指令运行：git config –global push.default matching或者git config –global push.default simple命令，以后再push就不会有警告。

下面说一下push.default matching和push.default simple的区别：

push.default设置maching的意思是：git push 会把你本地所有分支push到名称相对应的远程主机上。这意味着可能你会在不经意间push一些你原本没打算push的分支。

push.default设置成simple的意思是：git push仅仅把当前所在分支push到从当初git pull pull下来的那个对应分支上，另外，这个过程也会同时检查各个分支的名称是否相对应。

详细说明：http://stackoverflow.com/questions/13148066/warning-push-default-is-unset-its-implicit-value-is-changing-in-git-2-0

可以直接参考hiho一下的详细解答：http://hihocoder.com/discuss/question/2736/

下面是我的解题报告：

1.该题主要是统计三种颜色的字母的个数，red，yellow，blue；

2.需要注意的是，必须要判断字符是否为字母的情况，题目提到空格不加入统计。

3.思路：

使用栈存储和消除颜色，如果遇到<XXX>，则压入栈，如果遇到</XXX>，则pop出栈顶的元素，字母的颜色即栈顶的颜色。如果栈为空，则字母不统计。

样例输入

<yellow>aaa<blue>bbb</blue>ccc</yellow>dddd<red>abc</red>

样例输出

3 6 3

 
AC代码：
[c language=”++”]

//#include<string>
//#include<stack>
//#include<unordered_set>
//#include <sstream>
//#include "func.h"
//#include <list>
#include <iomanip>
#include<unordered_map>
#include<set>
#include<queue>
#include<map>
#include<vector>
#include <algorithm>
#include<stdio.h>
#include<iostream>
#include<string>
#include<memory.h>
#include<limits.h>
#include<stack>
using namespace std;

int getTagColor(string &str, int start)
{//红色返回0，黄色返回1，蓝色返回0
if (start < str.size())
{
if (start < str.size())
{
if (str[start] == ‘r’&&
start + 2 < str.size() &&
str[start + 1] == ‘e’&&
str[start + 2] == ‘d’)
return 0;
else if (str[start] == ‘y’&&
start + 5 < str.size() &&
str[start + 1] == ‘e’&&
str[start + 2] == ‘l’&&
str[start + 3] == ‘l’&&
str[start + 4] == ‘o’&&
str[start + 5] == ‘w’)
return 1;

else if (str[start] == ‘b’&&
start + 3 < str.size() &&
str[start + 1] == ‘l’&&
str[start + 2] == ‘u’&&
str[start + 3] == ‘e’)
return 2;
else return -4;
}
else return -4;
}
else return -4;
}

int getTag(string &str, int start)
{//获得标签的属性即颜色，属性包括颜色是开始还是结束
if (start < str.size())
{
if (str[start] == ‘<‘)
{
//颜色结束
if (start + 1 < str.size() && str[start + 1] == ‘/’)
return getTagColor(str, start + 2) + 3;
//颜色开始
else
return getTagColor(str, start + 1);
}
else return -1;
}
else return -1;
}

int main(void)
{
string text;
getline(cin , text);

stack<int> colorTag;
int times[3] = { 0 };
for (int i = 0; i < text.size(); i++)
{
int tag = getTag(text, i);
if (tag >= 0)
{
if (tag >= 3 && !colorTag.empty())
{//为颜色结束
colorTag.pop();
if (tag == 3) i += (3 + 2); //红色，跳过5个字符，包括’/’和最后的’>’
else if (tag == 4) i += (6 + 2);//黄色，跳过8个字符
else if (tag == 5) i += (4 + 2);//蓝色，跳过6个字符
}
else if (tag >= 0)
{
colorTag.push(tag);
if (tag == 0) i += (3+1); //红色，跳过3个字符，包括最后的’>’
else if (tag == 1) i += (6+1);//黄色，跳过6个字符
else if (tag == 2) i += (4+1);//蓝色，跳过4个字符
}
}
else if (!colorTag.empty() &&( (text[i] >= ‘a’&&text[i] <= ‘z’) || (text[i] >= ‘A’&&text[i] <= ‘Z’)))
{//栈不为空，需要注意判断为字母，题目提到空格不统计
times[colorTag.top()]++;
}
}
printf("%d %d %d\n", times[0],times[1], times[2]);
return 0;
}

[/c]

最大k乘问题

设I是一个n位十进制整数。如果将I划分为k段，则可得到k个整数。这k个整数的乘积称为I的一个k乘积。设计一个算法，对于给定的I和k，求出I 的最大k乘积。

一、思路：

1）我们定义dp[i][j]为数字I的前i为分成j段时的最大j乘积，如数字123，则dp[1][1]=1，dp[2][1]=12，dp[3][1]=123，dp[2][2]=2，如此类推。

 

2）那么我们来推导dp[i][j]与dp[i-x][j-1]，其中x<i，假设我们已经知道所有m<i，n<j取值时的dp[m][n]，构成dp[i][j]的可能为dp[i-1][j-1]*num[1..i]，dp[i-2][j-1]*num[2..i]，dp[i-3][j-1]*num[3..i]，dp[i-4][j-1]*num[4..i]……

所以我们把数字num[123…x….i]分为两部分，其中第一部分为num[123…i-x]，第一部分的最大乘积为dp[i-x][j-1]，第二部分为num[x..i]，则dp[i][j]=max(dp[i-x][j-1]* num[x..i])。

 

3）经过上述分析，我们可以把求I的最大k乘积划分为若干个子问题，这些子问题均为求最大乘积问题，然后通过这些最大乘积计算出I的最大k乘积，满足动态规划的最有自结构和无后向性性质。

 

4）已知数字I的位数为n，通过上述分析，求取dp[i][j]需要遍历O（n），计算dp[1][1]到dp[n][k]需要遍历O（n*k）的时间复杂度，总共需要O（n*n*k）的时间复杂度。

 

下列测试通过暴力搜索进行比较，验证了算法的正确性：

1234567890	最优分解	最大k乘积
k=1	1234567890	1234567890
k=2	12345678 90	1111111020
k=3	1234567 8 90	888888240
k=4	123456 7 8 90	622218240
k=5	12345 6 7 8 90	373312800
k=6	1234 5 6 7 8 90	186580800
k=7	123 4 5 6 7 8 90	74390400
k=8	12 3 4 5 6 7 8 90	21772800
k=9	1 2 3 4 5 6 7 8 90	3628800
k=10	1 2 3 4 5 6 7 8 9 0	0

二、复杂度分析

根据上述算法，时间复杂度为O（n*n*k），空间复杂度为O（n*k）。

三、源代码：

[c language=”++”]
//#include<string>
//#include <iomanip>
#include<set>
#include<queue>
#include<map>
//#include<unordered_set>
#include<unordered_map>
//#include <sstream>
//#include "func.h"
//#include <list>
#include<stdio.h>
#include<iostream>
#include<string>
#include<memory.h>
#include<limits.h>
#include<stack>
#include<vector>
#include <algorithm>
using namespace std;

/*
函数名 ：str2long
函数功能：把str转化long long
*/
long long str2long(string str)
{
long long result = 0;
for (int i = 0; i < str.size(); i++)
{//逐位转化
result = result * 10 + str[i] – ‘0’;
}
return result;
}
/*
函数名 ：devideNumber
函数功能：求出str的最大k乘积
*/
long long devideNumber(string I, int k, vector<vector<int>>&trace)
{
//n表示I的位数
int n = I.size();
//dp[i][j]表示把I前i位分成j段时的最大乘积
vector<vector<long long>> dp(I.size()+1, vector<long long>(k+1));

//初始化分成1段的时候
for ( int i = 1; i <=n; i++)
dp[i][1] = str2long(I.substr(0,i));

//求解dp[i][j]，其中j<=i，i位数字最多划分为i段，所以j不超过i
for (int i = 2; i <=n; i++)
{
for (int j = 2; j <=k && j<=i; j++)
{
long max=0;
for (int m = 1; m < i; m++)
{//把前i位分为两部分，一部分是0~m-1，另外一部分是m~i
int tmp = dp[m][j – 1] * str2long(I.substr(m, i-m));
if (tmp >=max)
{
max = tmp;
//trace的意义是dp[i][j]取得最大值时，最后一个数字为m~i-1
trace[i][j] = m;
}
}
dp[i][j] = max;
}
}
return dp[I.size()][k];
}

int main(void)
{
cout << "|—————————————————————————|\n";
cout << "| 算法实现题7 |\n";
cout << "| |\n";
cout << "| 设 I 是一个n位十进制整数，如果把I划分为k段，则可得到k个整数。 |\n";
cout << "| 这k个整数的乘积称为I的一个k乘积。给定I和k，求出I的最大k乘积。 |\n";
cout << "| |\n";
cout << "|—————————————————————————|\n";
while (1)
{
string I;
int k;
cout << "请输入I的值(输入负数退出)：" << endl;
cin >> I;
if (I[0] == ‘-‘) break;
cout << "请输入划分的段数k：" << endl;
cin >> k;

//异常检测
if (I.size() < k)
{
cout << "输入不合要求！k不能超过I的位数！"<<endl<<
"您输入的I的位数为" << I.size() << "，k的值为" << k << "，请重新输入。" << endl << endl;
continue;
}
else if (k < 1)
{
cout << "k的取值至少为1！请重新输入！" << endl;
}

//trace记录I求出最大k乘积后，每个位置所取的位数
vector<vector<int>> trace(I.size()+1,vector<int>(k+1));
int result=devideNumber(I, k, trace);
cout << "最大k乘积为：" << endl << result << endl;

//回溯分成的段
stack<string> sta;
int tmp = I.size();
for (int i = 0; i < k; i++)
{//通过trace把分成的段记录下来
sta.push(I.substr(trace[tmp][k – i], tmp – trace[tmp][k – i]));
tmp = trace[tmp][k – i];
}
cout << "分成的各段为：" << endl;
while (!sta.empty())
{
cout << sta.top() << " ";
sta.pop();
}
cout << endl<<endl;
}
return 0;
}

[/c]